logic_circuit_example in CircuiTikZ LaTeX

Draw a Logic Circuit in CircuiTikZ

by
  • In this tutorial, we will learn how to draw a logic circuit in LaTeX using CircuitikZ package with different electrical components styles: American, European and IEEE. The circuit example has been suggested by Nithin Aaron, Thanks to him!
logic_circuit_example in CircuiTikZ LaTeX

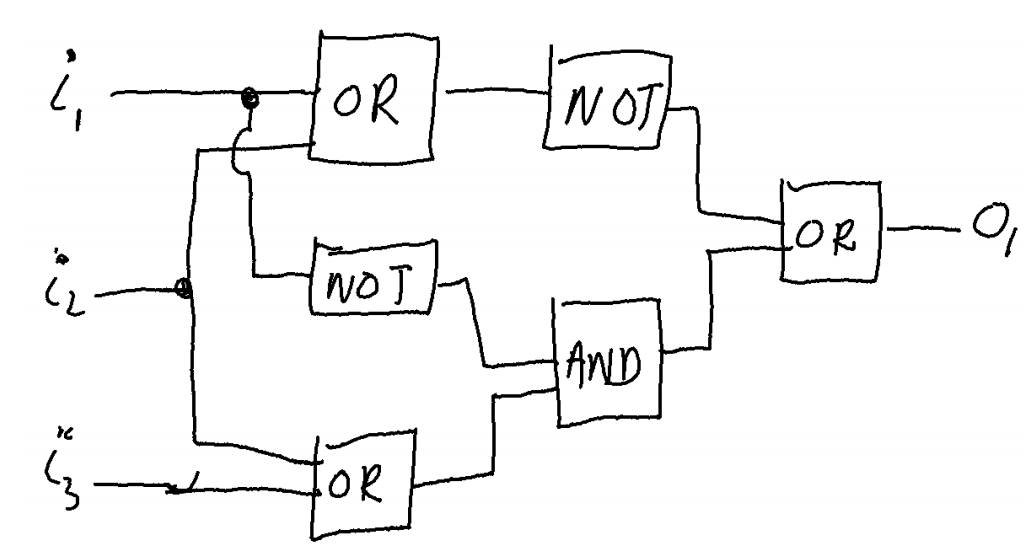
Hand drawn circuit suggested by Nithin Aaron 

If you enjoy these TikZ tutorials, Please consider supporting me by buying me a coffee ❤️

Buy Me a Coffee at ko-fi.com

Short description

  • The logic circuit consists of OR, AND and NOT logic gates. All these elements can be added using \node command. Components can be customized using the command \ctikzset {}. To modify the components style use logic ports = ieee or (american, or european) inside the previous command. Using logic ports/scale =0.8 reduces the default size by 20%. The option logic ports/fill=lightgray changes the filling color of all logic gates. The jump crossing is a node element and can be also drawn along the path. Check the code below for more details!

LaTeX code of the Logic circuit: IEEE style

 \documentclass[border=0.2cm]{standalone}

% Required packages and libraries
\usepackage{circuitikz}
\usetikzlibrary{calc}

\begin{document}


\begin{tikzpicture}

% Circuit style
\ctikzset{
	logic ports=ieee,
	logic ports/scale=0.8,
	logic ports/fill=lightgray
}

% Logic ports
\node[or port] (ORa) at (0,0){};
\node[not port] (Noa) at (0,-2){};
\node[or port] (ORb) at (0,-4){};

\node[not port] (Nob) at (2.5,0){};
\node[and port] (ANDa) at (2.5,-3){};

\node[or port] (ORc) at (5,-1.5){};

% Connection
\draw (ORa.out) -- (Nob.in);

\draw (Noa.out) -| (ANDa.in 1);
\draw (ORb.out) -| (ANDa.in 2);

\draw (ANDa.out) -|  (ORc.in 2);
\draw (Nob.out) -| (ORc.in 1);
\draw (ORc.out) -- ++(1,0) node[near end,above]{Out};

\draw (ORa.in 1) -- ++(-1.5,0)node[left](In1){In1};
\draw (ORb.in 2) -- ++(-1.5,0)node[left](In3){In3};

% Jump crossing element
\node at (ORa.in 2)
[
	below,
	jump crossing,
	rotate=-90,
	scale=1.3
](X){};

\draw (Noa.in) -| (X.east)
	(X.west) to[short,-*] (X.west |- ORa.in 1); 

\draw ($ (In1) !.5! (In3) $) node[]{In2}
	++ (0.4,0) to[short,-*] ++(0.5,0) coordinate(a)
	|- (X.south) (a) |- (ORb.in 1);
\end{tikzpicture}


\end{document}
  • How can I get coordinates of the half distance between two nodes? To make the circuit drawing flexible, IN2 should be put in the half distance between IN1 and IN3 and from there we continue drawing the circuit. This can be achieved thanks to the calc library by using the syntax: ($ (In1) !.5! (In3) $). (IN1) is the saved coordinates of the first node and (IN3) is the saved coordinates of the second node.

Compiling the above code yields:

Logic Circuit in CircuiTikZ IEEE style

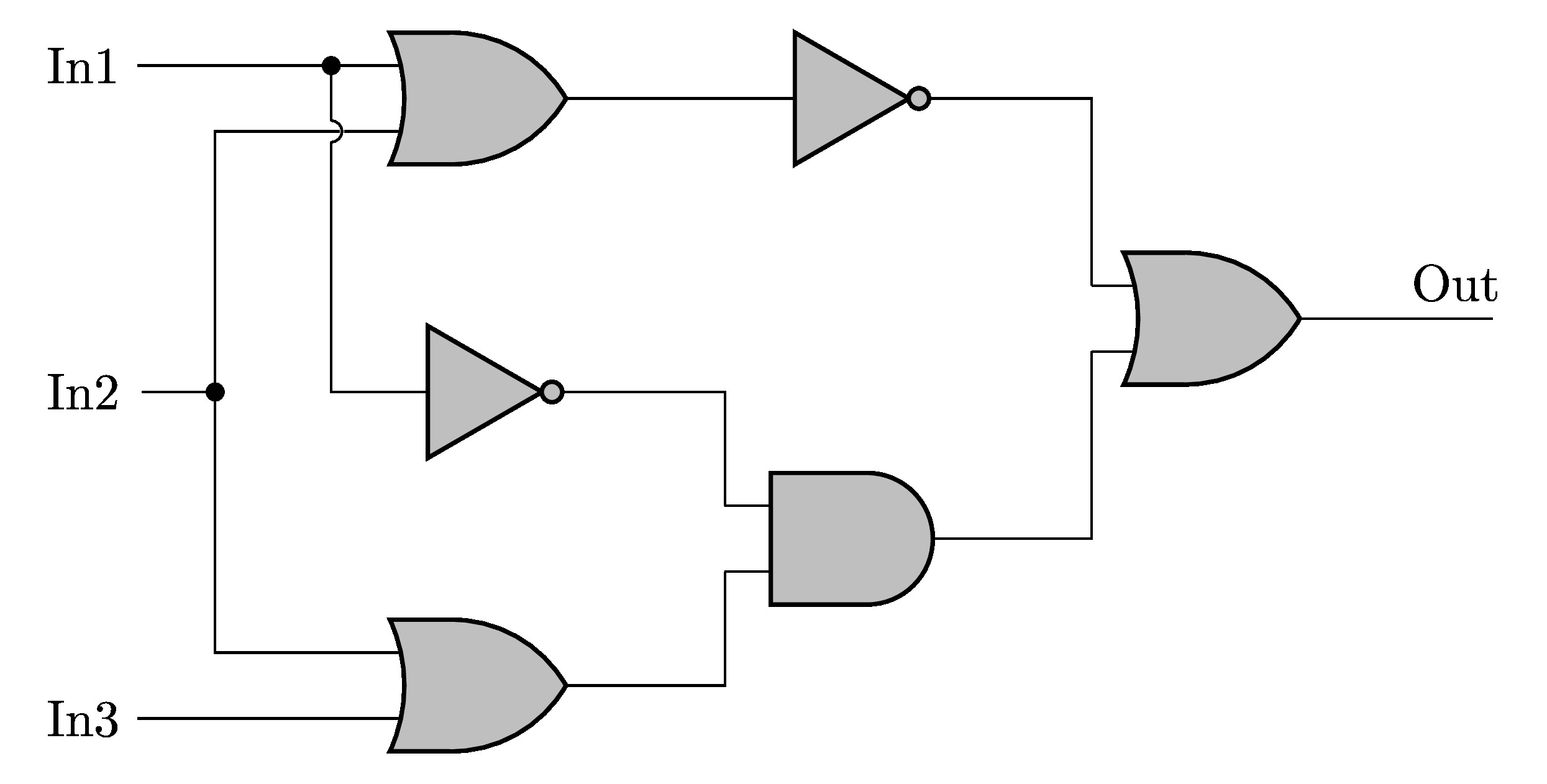
Logic Circuit in CircuitikZ with IEEE components style

View Image
TeX code
Open in Overleaf

LaTeX code of the Logic circuit: American style

By changing the style from ieee to american in the above code, we will get:

Logic Circuit in CircuiTikZ American style

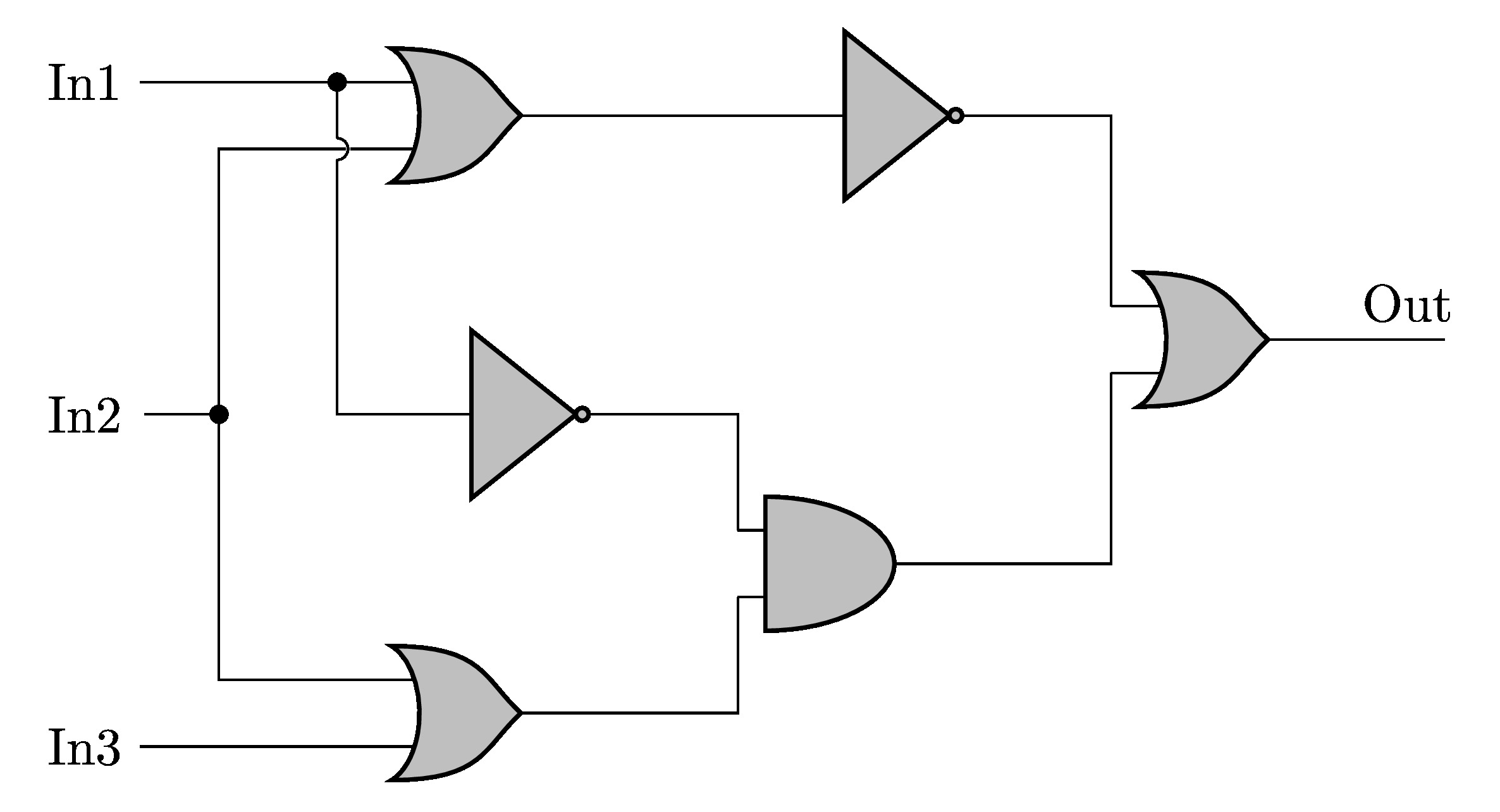
Logic Circuit in CircuitikZ with American components style

LaTeX code of the Logic circuit: European style

By changing the style from ieee to european in the above code, we will get:

Logic Circuit in CircuiTikZ European style

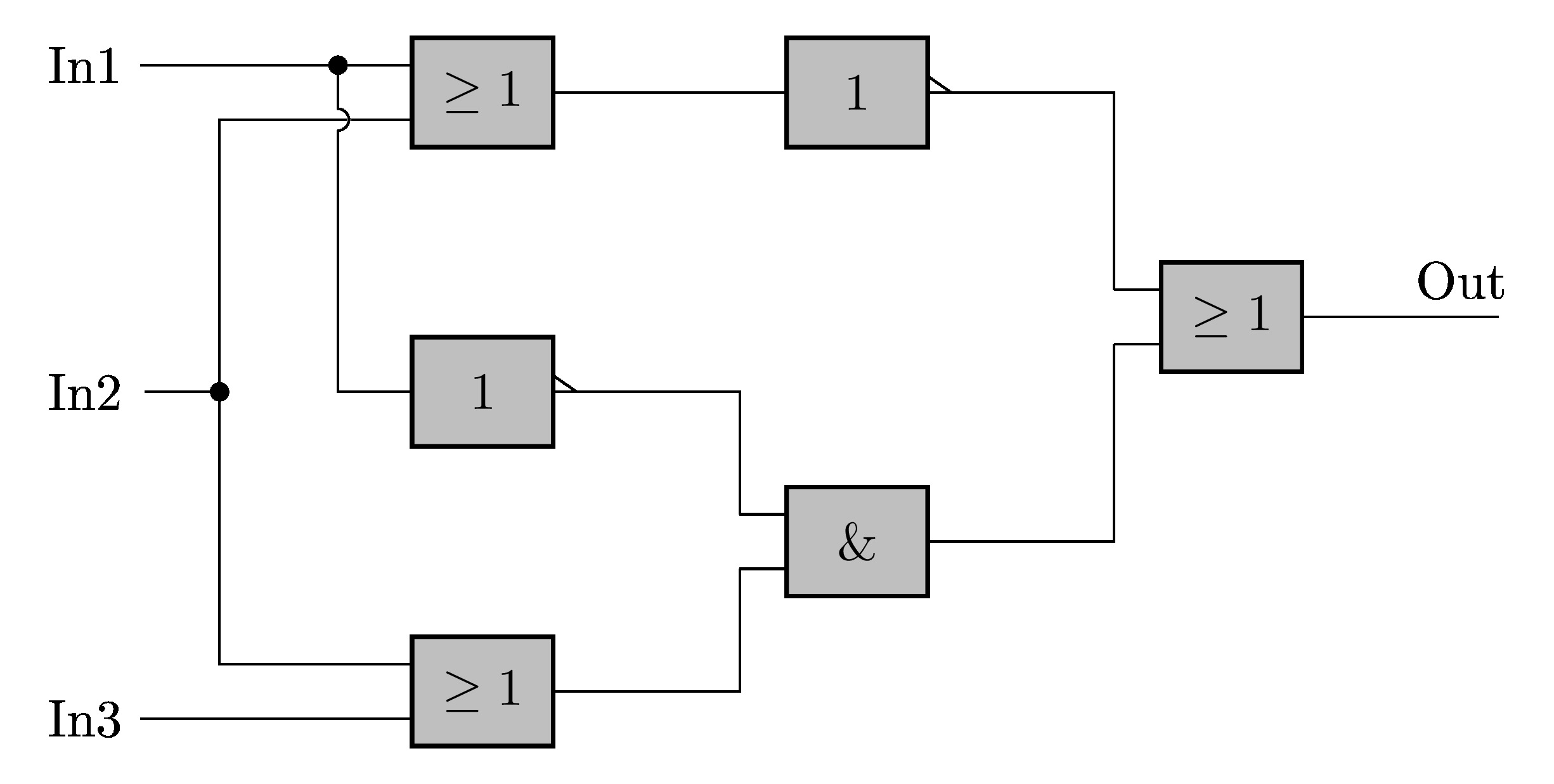
Logic Circuit in CircuitikZ with European components style

  • If you would to see a detailed tutorial about it, leave me a comment below or reach me via e-mail at admin@latexdraw.com, I will be happy to hear from you!

2 thoughts on “Draw a Logic Circuit in CircuiTikZ”

  1. It’s not the scope of this site, but did you try to figure out the logical behaviour of that thing?

    SPOILER
    It’s just an inverter for i₁.

    • Hey Moss!
      That’s correct, and here is a detailed answer for future curious minds:
      Let’s consider the algebraic notation:
      + for OR gate, * for AND gate, ! for NOT gate.
      We have:
      !(a + b) + (!a * (b + c))
      !a * !b + !a * b + !a * c
      !a * (!b + b) + !a * c
      It should be noted that !b + b is always true. Therefore, this is equal to:
      !a + !a * c
      But the right side being true implies the left side is also true. Therefore, we can say it’s just:
      !a
      Source: Bassel Toubbeh from “It’s in LaTeX so it must be true” facebook group.

Comments are closed.